2022(西安)微分方程与动力系统

学术会议II

程 序 册

中国·西安

2022年11月25日--11月27日

 

本次学术会议旨在邀请微分方程与动力系统及相关领域专家学者分享最新研究成果，进一步探讨微分方程与动力系统中的前沿问题，促进学术交流与合作。学术会议的主题涉及时滞微分方程、反应扩散方程、动力系统等相关领域。

本次学术会议由西安电子科技大学发展规划部与best365亚洲版登录主办，受国家自然科学基金、陕西省杰出青年科学基金、中国博士后科学基金特别资助等项目支持。

受疫情影响，本次会议以线上方式进行。欢迎大家参加！

会议时间：2022年11月25-27日

会议方式：腾讯会议ID：992 6304 7966 密码：123456

组织委员会：马如云 吴事良 李善兵 常永奎 白振国 薄伟健 李 燕 李芳 祁世杰 王 烽

会议联系人：

马如云 13038744011 mary@nwnu.edu.cn

吴事良 18392190403 slwu@xidian.edu.cn

李善兵 18700410622 lishanbing@xidian.edu.cn

主办单位：

西安电子科技大学发展规划部

西安电子科技大学best365亚洲版登录

特邀嘉宾(按姓氏拼音排序)：

    白学利     西北工业大学

包雄雄     长安大学

    储继峰     上海师范大学

    丁维维     华南师范大学

            杜一宏      澳大利亚新英格兰大学

       方健      哈尔滨工业大学

                冯兆生      美国德克萨斯大学-RGV分校

    高道舟      上海师范大学

郭宏骏      同济大学

    韩茂安      浙江师范大学

    黄继才      华中师范大学

    黄建华      国防科技大学

黄启华      西南大学

    霍海峰      兰州理工大学

      蒋卫华      哈尔滨工业大学

靳祯       山西大学

李芳       中山大学

   李 骥      华中科技大学

   李雪梅     湖南师范大学

连增      四川大学

林国      兰州大学

林支桂     扬州大学

    柳振鑫      大连理工大学

    娄本东     上海师范大学

吕克宁     四川大学

   马满军     浙江理工大学

    倪明康     华东师范大学

     彭锐      浙江师范大学

      盛伟杰     哈尔滨工业大学

     舒洪英     陕西师范大学

    宋永利      杭州师范大学

孙桂全      中北大学

 孙建文      兰州大学

    陶有山      上海交通大学

 王宾国      兰州大学

            王佳兵      中国地质大学（武汉）

王其如      中山大学

    王荣年      上海师范大学

王智诚      兰州大学

    吴建华      陕西师范大学

    吴雅萍      首都师范大学

    向昭银      电子科技大学

        易泰山      中山大学（珠海）

 张 亮      兰州大学

    张文萌      重庆师范大学

        赵育林      中山大学（珠海）

周茂林      南开大学

 

2022(西安)微分方程与动力系统学术会议II

11月25日 腾讯会议ID：992 6304 7966 密码：123456

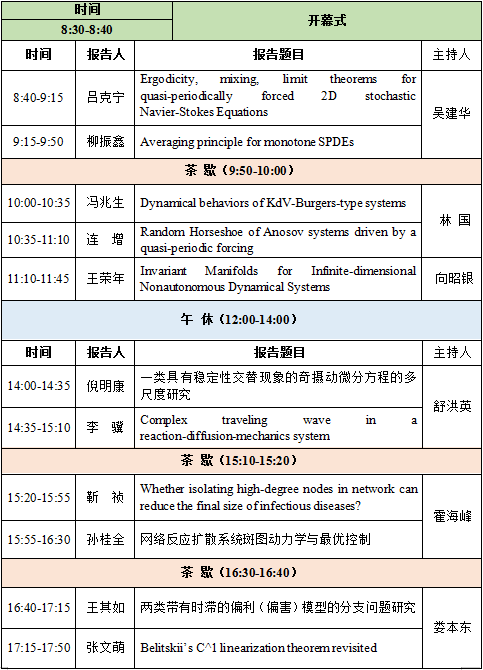
11月26日  腾讯会议ID：992 6304 7966  密码：123456

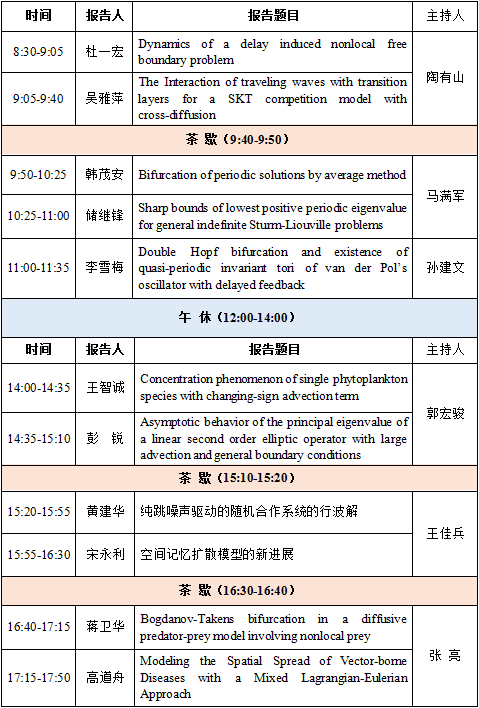
11月27日  腾讯会议ID：992 6304 7966  密码：123456

 

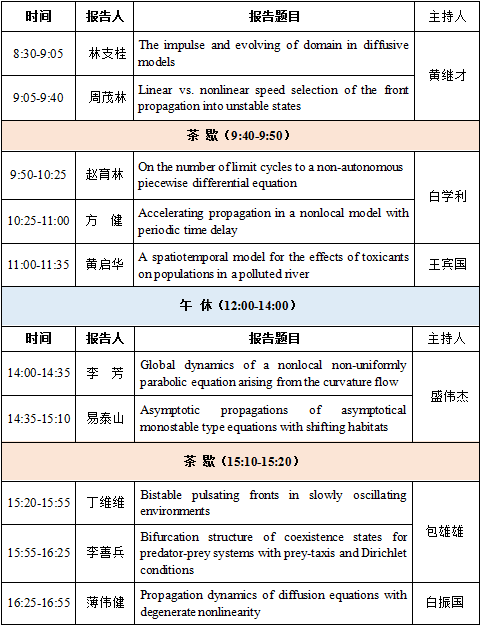
报告题目与摘要(以姓氏拼音为序)

2022(西安)微分方程与动力系统学术会议II

Propagation dynamics of diffusion equations with degenerate nonlinearity

薄伟健 西安电子科技大学

In this talk, we consider the propagation dynamics of diffusion equations with degenerate nonlinearity, which includes the traveling wave solutions and asymptotic spreading of degenerate delayed equations and degenerate Lotka-Volterra competition systems.

Sharp bounds of lowest positive periodic eigenvalue for general indefinite Sturm-Liouville problems

储继峰 上海师范大学

The aim of this paper is to obtain the sharp estimates for the lowest positive periodic eigenvalue of a general Sturm-Liouville problem with an indefinite potential. A typical example of such problems is the well-known Camassa-Holm equations with indefinite potentials. It is shown that the solution of the minimization problem of the lowest positive periodic eigenvalue will lead to more general distributions of potentials which have no densities with respect to the Lebesgue measure. As a result, it is very natural to choose the general setting of the measure differential equations to understand the eigenvalues and their minimization. The variational characterization of the lowest positive periodic eigenvalues, together with a strong continuous dependence of eigenvalues on the potentials, will play crucial roles in our analysis.

Bistable pulsating fronts in slowly oscillating environments

丁维维 华南师范大学

In this talk, I will present some recent progress on reaction-diffusion fronts in spatially periodic bistable media. The results include: existence of pulsating fronts with large periods, existence of and an explicit formula for the limit of front speeds as the spatial period goes to infinity, convergence of pulsating front profiles to a family of front profiles associated with spatially homogeneous equations. This talk is mainly based on a joint work with Francois Hamel and Xing Liang.

Dynamics of a delay induced nonlocal free boundary problem

杜一宏 澳大利亚新英格兰大学

We consider the dynamics of a population with an age structure whose population range expands with time, where the adult population is assumed to satisfy a reaction-diffusion equation over a changing interval determined by a Stefan type free boundary condition, while the juvenile population satisfies a reaction-diffusion equation whose evolving domain is determined by the adult population. The interactions between the adult and juvenile populations involve a fixed time-delay, which renders the model nonlocal in nature. In this talk I will show the well-posedness of the model and present a rather complete description of its long-time dynamical behavior, which follows a spreading-vanishing dichotomy. When spreading persists, we show that the population range expands with an asymptotic speed, which is uniquely determined by an associated nonlocal elliptic problem over the half line. This talk is based on a recent joint work with Jian Fang (HIT) and Ningkui Sun (Shandong Normal Univ).

Accelerating propagation in a nonlocal model with periodic time delay

方健 哈尔滨工业大学

In this talk, we investigate the accelerating propagation dynamics of a nonlocal model with periodic time delay, which arises from the study of stage-structured invasive species subject to seasonal successions.

Dynamical Behaviors of KdV-Burgers-type Systems

冯兆生 美国德克萨斯大学-RGV分校

In this talk, we consider dynamics of a class of the KdV-Burgers-type systems by starting with Burgers-type equations, and then focus on the higher-order KdV-Burgers equation, a partial differential equation that occupies a prominent position in describing some physical processes in motion of turbulence and other unstable process systems. We limit our attention to various wave phenomena and their asymptotic behaviors based on the bifurcation theory and dynamical analysis.

Modeling the Spatial Spread of Vector-borne Diseases with a Mixed Lagrangian–Eulerian Approach

高道舟 上海师范大学

Vector-borne diseases such as malaria, dengue fever and Lyme disease remain one of the major global health threats. In this talk, based on the classical Ross–Macdonald model, we develop a multi-patch and multi-group model to study the effects of human commuting and/or mosquito migration on the spread of vector–borne diseases. We first define the basic reproduction number of the model, R0, which completely determines the global dynamics of the model system. Then we explore the influence of host and/or vector movement on the disease persistence and show that the basic reproduction number has upper and lower bounds which are independent of the host residence times matrix and the vector migration matrix. In particular, nonhomogeneous mixing of hosts and vectors in a homogeneous environment increases disease persistence and the basic reproduction number of the model attains its minimum when the distributions of humans and mosquitoes are proportional. In two-group and two-patch case, we numerically analyze the dependence of the basic reproduction number and the total number of infected people with respect to the residence times matrix and investigate the optimal vector control strategy with limited resources.

Bifurcationofperiodicsolutionsby average method

韩茂安 浙江师范大学

This talk concerns an introduction to the average method in the study of periodic solutions of periodic equations, including new advances obtained recently.

纯跳噪声驱动的随机合作系统的行波解

黄建华 国防科技大学

该报告先用大偏差原理推导出广义Feynman－Kac公式，在研究分布意义下建立纯跳噪声驱动的KPP方程的行波解的存在性和渐近波速估计上下界估计,分析噪声对传播速度的影响。最后运用随机单调动力系统理论和上、下解技巧等方法讨论纯跳噪声驱动的随机合作系统行波解的存在性和渐近传播速度的上、下界估计，该工作是与文豪和黎育红合作完成。

A spatiotemporal model for the effects of toxicants on populations

in a polluted river

黄启华 西南大学

One reason why polluted water is the world's primary concern is because it persists to pose threats to the health of aquatic life. To study the effects of environmental toxicants on population dynamics in polluted rivers, we develop a process-oriented model that describes the interaction between a population and a toxicant in an advective environment. The model consists of two reaction-diffusion-advection equations, one of which governs the dispersal and growth of the population under the influence of toxicants, while the other describes the dispersal, input, as well as decay of the toxicant. We explore the existence and stability of steady states based on the analysis of eigenvalue problems, which yields sufficient conditions that lead to population persistence or extinction. We numerically analyze how the interplay between several factors (toxicant input, flow velocity, the diffusion and advection characteristics of the population and the toxicant) affects the persistence and spatial distribution of the population.

Bogdanov-Takens bifurcation in a diffusive predator-prey model involving nonlocal prey

蒋卫华 哈尔滨工业大学

Firstly, an explicit formula for the coefficients of normal form for Bogdanov-Takens bifurcation in PFDEs are presented. Then, for a diffusive predator-prey model involving nonlocal prey, the critical condition for the destabilization of the coexistence equilibrium is established, which indicates that the coexistence equilibrium can lose its stability through Turing, Hopf, Bogdanov-Takens, Turing-Hopf and Hopf-Hopf bifurcations. Further, tri-stable spatio-temporal inhomogeneous patterns are theoretically predicted, and also shown numerically. This talk is based on a joint work with Dr. Xun Cao and Dr. Xianyong Chen.

Whether isolating high-degree nodes in network can reduce the final size of infectious diseases?

靳祯 山西大学

It has been a challenge to formulate network-based control measures on infectious diseases, especially on emerging diseases, due to the complexity of the network topology. Generally, isolating high-degree nodes is one of the intuitive intervention measures. The final size and the epidemic duration are two vital evaluation indices of infectious diseases severity, but the last one has not been explicitly calculated so far in network-based models. Therefore, in this talk, we introduced the effects of two measures of isolating high-degree nodes at different time-complete isolation and incomplete isolation, on these two indices. We applied the reducing-dimension method to convert the mean-field model in networks into an equivalent and simpler low-dimension model, and then calculated the exact expression of the final size and the epidemic duration. We found that, in complete isolation the final size always reduces but there exists an isolation time threshold of the epidemic duration in some cases, before that such a strategy lengthens the epidemic duration, and otherwise shortens that period. In contrast, in incomplete isolation the epidemic duration always increases but there exists an isolation time threshold of the final size, before which, the incomplete isolation reduces the final size, and otherwise increases the final size. This result provides a new insight into controlling infectious diseases in network.

Global dynamics of a nonlocal non-uniformly parabolic equation

arising from the curvature flow

李芳 中山大学

In this talk, we discuss a type of non-uniformly parabolic problem with nonlocal term arising from the curvature flow. First the classification of the finite-time blow-up/global existence phenomena based on the associated energy functional and explicit expression of all nonnegative steady states are demonstrated. More importantly, we derive that any bounded solution converges to some steady state as time goes to infinity. The difficulties in proving this convergence result lie in the existence of a continuum of steady states and the lack of the comparison principle due to the introduction of nonlocal term. To conquer these difficulties, we combine the applications of Lojasiewicz-Simon inequality and energy estimates.

Complex traveling wave in a reaction-diffusion-mechanics system

李骥 华中科技大学

We analyze the stability of traveling pulse in a reaction-diffusion-mechanicsSystem modeling cardiac cell. This system consists of amodified FitzHugh-Nagumo system bidirectionally coupling with an elasticity equation. Applying the framework of geometric singular perturbation theory, we analyze the spectrum of simple traveling pulse as well as multiple front/back in this system and prove it is linearly stable. The main tool is exponential dichotomies and Melnikov method. The existence of multi-pluse, is proved by showing that there is a double twist heteroclinic loop structure.

Bifurcation structure of coexistence states for predator-preysystems with prey-taxis and Dirichlet conditions

李善兵 西安电子科技大学

In this talk, the stationary problem of predator-prey systems with prey-taxis in a bounded domain is considered. Under homogeneous Dirichlet boundary conditions, we make a detailed description for the global bifurcation structure of coexistence states and find the ranges of parameters for which there exist coexistence states.

Double Hopf bifurcation and existence of quasi-periodic invariant tori of van der Pol’s oscillator with delayed feedback

李雪梅 湖南师范大学

In this work, we analyse the double Hopf bifurcation of van der Pol’s oscillator with delayed feedback based on the center manifold theorem and normal form theory. Then we prove the persistence of quasi-periodic invariant tori in the double Hopf bifurcation under perturbations by using KAM theory.

Random Horseshoe of Anosov systems driven by a quasi-periodic forcing

连增 四川大学

Consider C2 Anosov systems on a compact manifold driven by a quasiperiodic forcing. We study their dynamical complexity on various levels from both perspectives of path-wise dynamics and stochastic processes. In this talk, I will report the results on the existence of random horseshoe from two different viewpoints：topology and probability. This is joint with Wen Huang and Kening Lu.

The impulse and evolving of domain in diffusive models

林支桂 扬州大学

In order to understand how the combination of domain evolution and impulsive harvesting affect the dynamics of a population, we propose a diffusive logistic population model. Initially the ecological reproduction index of the impulsive problem is introduced and given by an explicit formula, which depends on the domain evolution rate and the impulsive function. Then the threshold dynamics of the population under monotone or nonmonotone impulsive harvesting is established based on this index. Finally numerical simulations are carried out to illustrate our theoretical results, and reveal that a large domain evolution rate can improve the population survival, no matter which impulsive harvesting takes place. Contrary, impulsive harvesting has a negative effect on the population survival, and can even lead to the extinction of the population. Some impulsive diffusive models are also proposed.

Averaging principle for monotone SPDEs

柳振鑫 大连理工大学

The first Bogolyubov theorem on averaging for SDEs has been investigated extensively. In this talk, we will discuss the second Bogolyubov theorem and global averaging principle for monotone SPDEs. This talk is based on our joint work with Mengyu Cheng.

Ergodicity, mixing, limit theorems for quasi-periodically forced 2D stochastic Navier-Stokes Equations

吕克宁 四川大学

We consider the incompressible 2D Navier-Stokes equations on the torus driven by a deterministic time quasi-periodic force and a noise that is white in time and extremely degenerate in Fourier space. We show that the asymptotic statistical behavior is characterized by a uniquely ergodic and exponentially mixing quasi-periodic invariant measure. The result is true for any value of the viscosity $\nu>0$. By utilizing this quasi-periodic invariant measure, we show the strong law of large numbers and central limit theorem for the continuous time inhomogeneous solution processes. Estimates of the corresponding rate of convergence are also obtained, which is the same as in the time homogeneous case for the strong law of large numbers, while the convergence rate in the central limit theorem depends on the Diophantine approximation property on the quasi-periodic frequency and the mixing rate of the quasi-periodic invariant measure. We also prove the existence of a stable quasi-periodic solution in the laminar case (when the viscosity is large). This talk is based on a joint work with Liu Rongchang.

一类具有稳定性交替现象的奇摄动微分方程的多尺度研究

倪明康 华东师范大学

该报告将介绍一类退化方程具有稳定性交替现象的奇摄动两点边值问题，用吹胀法定性地分析了在临界流形和转点附近的方程轨线动力学性态。作者将利用正则化方法和非标准边界层函数方法构造该问题的一致有效渐近展开式，并使用微分不等式的方法证明该问题解的存在性，并给出渐近解的一致有效估计。

Asymptotic behavior of the principal eigenvalue of a linear second order elliptic operator with large advection and general boundary conditions

彭锐 浙江师范大学

In this talk, we shall report our recent progress on a linear second order elliptic operator with gradient field and the Dirichlet boundary condition or general Robin boundary condition. When $N\geq2$, under proper conditions on the advection function $m$, we establish the asymptotic behavior of the principal eigenvalue as the advection coefficient $\alpha\to\infty$, and when $N=1$, we obtain a complete description for such asymptotic behavior provided $m'$ changes sign at most finitely many times. Our results complement and improve those by Berestycki, Hamel and Nadirashvili (CMP, 2005), Chen-Lou (IUMJ, 2008), P.-Zhou(IUMJ, 2018), and also answer some questions raised by Berestycki, Hamel and Nadirashvili (CMP, 2005).

空间记忆扩散模型的新进展

宋永利 杭州师范大学

首先，介绍空间记忆扩散模型的生物学背景及数学建模思想。其次，介绍单种群空间记忆模型的研究现状及相关动力学，特别是给出记忆时滞和非局部空间竞争联合作用导致的Turing-Hopf分支，双Hopf分支的动力学性质。最后，我们介绍具有空间记忆扩散的资源-消耗模型的稳定性及分支分析的相关结果。

网络反应扩散系统斑图动力学与最优控制

孙桂全 中北大学

斑图动力学是非线性动力学的主要研究内容之一，广泛用于数学、物理学、化学、生物学、生态学、计算机科学等多个领域。例如，传染病斑图有助于识别传染病暴发的热点区域，揭示传染病传播规律和时空分布特征。目前关于反应扩散系统斑图的研究多集中在连续空间基于标准布朗运动的反应扩散方程。然而，种群分布的离散型、扩散的异质性与大尺度长距离等特征不符合标准的布朗运动，不适合利用反应扩散方程对此类反应扩散过程建模。复杂网络通常具有小世界、异质性等特征，网络反应扩散系统为更精确刻画反应扩散过程提供了可能。本报告首先讨论网络反应扩散系统Turing斑图，给出网络平均度与斑图结构之间的定性定量关系。然后，基于微分方程最优控制理论，讨论斑图结构的最优控制策略。

两类带有时滞的偏利（偏害）模型的分支问题研究

王其如 中山大学

1.具有线性增长率和非线性功能反应函数的两物种偏利时滞模型的Hopf分支.

2.具有离散时滞和分布时滞的偏利（偏害）模型的横越分支与Hopf分支.

Invariant Manifolds for Infinite-dimensional Nonautonomous Dynamical Systems

王荣年 上海师范大学

In this talk we consider the existence of global finite-dimensional invariant manifolds for nonautonomous infinite-dimensionall dynamical system. Several applications are also mentioned.

Concentration Phenomenon of Single Phytoplankton Species with Changing-Sign Advection Term

王智诚 兰州大学

In this talk we investigate a nonlocal reaction-diffusion equation modeling the growth of phytoplankton species with changing-sign advection in a vertical water column, where the species depends solely on light for its metabolism. We mainly study the concentration phenomenon of the phytoplankton with large advection amplitude and small diffusion rate. Firstly, we study the threshold-type dynamics of the population by critical death rate. Secondly, we examine the concentration phenomenon with large advection amplitude and small diffusion in two cases: (i) the advection function changes sign only once from positive to negative in water column. We find that the phytoplankton will concentrate at certain critical point with large advection amplitude and small diffusion; (ii) the advection function $h(x)<0$ in $[0,\kappa)$ with $\int^{x}_{0}h(s)\mathrm{d}s<0$ for all $x\in(0,1]$, the phytoplankton will concentrate at the surface of water column with large advection amplitude and small diffusion. We also investigate the limiting distribution of phytoplankton as diffusion rate $D\rightarrow+\infty$, the phytoplankton tends to even distribution in water column.

The Interaction of Traveling Waves with Transition Layers for a SKT Competition Model with Cross-Diffusion

吴雅萍 首都师范大学

Consider the following SKT competition model

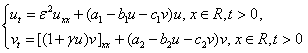
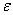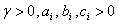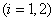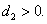with small diffusion rateand non-small cross diffusion rate,andBy applying geometric singular perturbation argument and topological index method, Yaping Wu and Ye Zhao proved that the system in strong competition case has a family of stable travelling waves connecting 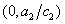and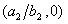 with locally unique slow speed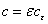and both components of the waves have transition layers.In this talk we shall mainly talk about our recent work on the higher order two-scale expansion of the waves with transition layer for small 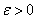and the long time behavior and the asymptotic speed of the shifts of twointeracting waves. It is a joint work with Dr. Hao Zhang (Capital Normal University) and Prof. Shin Ichiro Ei (Hokkaido University).

Asymptotic propagations of asymptotical monostable type equations with shifting habitats

易泰山中山大学(珠海)

We consider nonlinear propagation for the single species population in a shifting habitat subject to unbalanced resources. The population dynamics is modelled by a reaction-diffusion equation with an {\it asymptotical} KPP-type nonlinearity. Complicated dynamical patterns, naturally depending on the velocity of the shifting resource and the propagation velocities of the limiting systems at both $\infty$ and $-\infty$, emerge, and our focus is to characterize these patterns. We first characterize the persistence and extinction of an asymptotical Fisher-KPP type equation and then establish a key relationship between the asymptotical Fisher-KPP type and the asymptotical KPP type equations. These, together with comparison principles, enable us 1). to obtain asymptotic propagation behaviors of asymptotical KPP type equations and 2). to analyze and describe the influence of the velocity of the shifting resources and the propagation velocity of the limiting systems on the asymptotic propagations of the reaction-diffusion equation with an asymptotical KPP-type nonlinearity.

Belitskii’s C^1 linearization theorem revisited

张文萌重庆师范大学

Smooth linearization is one of the central themes in the study of dynamical systems. In this talk, we revisit Belitskii’s C^1 linearization theorem, which is one of the most famous theorems in the study of smooth linearization. We point out that the original proof of this theorem has some problems and take a different approach based on smooth invariant foliations to study this theorem for a larger class of dynamical systems, i.e., the random dynamical systems.

On the number of limit cycles to a non-autonomous piecewise differential equation

赵育林中山大学(珠海)

This paper is concerned with the non-autonomous piecewise differential equation defined by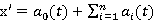, where 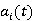arereal and 1-periodic 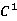functions. The main result is that, if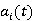,i=1,2,…,n，do not change sign and have the same sign in [0, 1], then the equationhas at most two limit cycles (isolated solutions satisfying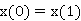).We also study all the possible configurations of limit cycles. In the same way, we extend the main result of at most two limit cycles to a class of general non-autonomous piecewise polynomial differential equation, and give a criterion for the uniqueness of the limit cycle is given for this equation. As an application, we estimate the number of limit cycles a class of piecewise smooth planar polynomial rigid system that the separation line is closed curve containing origin.

Linear vs. nonlinear speed selection of the front propagation

into unstable states

周茂林南开大学

In this talk, we consider the speed selection problem of the scalar reaction-diffusion equations and the Lotka-Volterra competition systems. Compared with the classical result on singleequations in [Lucia-Muratov-Novaga, CPAM 2004], we propose a sufficient and necessary criterion to this long-standing problem of monostable dynamical systems for the first time. Moreover,our results can further reveal the essence of the linear determined problem from a new viewpoint on the decay rate of travelling wave solutions.